Lehrstuhl Wissenschaftliches Rechnen
Das Anfangsdaten-Problem
Die Allgemeine Relativitätstheorie wird durch die Einsteinschen Feldgleichungen dargestellt, einem System aus zehn nichtlinearen, partiellen Differentialgleichungen. Sie beschreibt die Gravitation durch die Krümmung einer vierdimensionalen, pseudoriemannschen Mannigfaltigkeit. Testteilchen auf die keine Kraft einwirkt bewegen sich dann auf Geodäten durch diesen Raum. Arnowitt, Desner und Misner schlugen eine Zerlegung in einen dreidimensionalen, raumartigen Anteil und einen eindimensionalen, zeitartigen Anteil vor. Diese 3+1-Zerlegung macht klar, dass zur Lösung des Systems partieller Differentialgleichungen Anfangsdaten auf einer Hyperfläche zu einer gewissen Zeit t notwendig sind. Abgesehen von der Topologie und dem Energie-Impuls-Tensor, welche das zu lösende Problem charakterisieren, müssen bestimmteconstraints erfüllt werden. Diese ergeben sich
aus der Herleitung der 3+1-Zerlegung.
Betrachtet man isolierte schwarze Löcher, so gibt es keine Materie im Aussenraum und der Energie-Impuls-Tensor verschwindet. Das Gebiet auf welchem die Differentialgleichungen gelöst werden, ist nun abhängig vom jeweiligen Ansatz. Eine Variante besteht im Ausschneiden (excision ) des Innenraumes der Schwarzen
Löcher. Dieses Vorgehen geht auf Bowen und York (in [1]) zurück. In den
vergangenen Jahren haben sich zudem sogenannte punctures durchgesetzt. Durch eine geschickte
Separation des konformen Faktors verschwinden die Singularitäten und man kann
das Problem nun auf einem konvexen Gebiet lösen.
asymptotical flatness ) wird und dass man den
metrischen Tensor konform in einen skalaren Faktor und eine flache
Hintergrundmetrik zerlegen kann (conformal
flatness ). Des weiteren soll die Spur der extrinsischen Krümmung
verschwinden(maximal slicing ).
Diese Voraussetzungen werden allesamt auch für Punctures gemacht und es
ergibt sich folgende semilineare und skalare elliptische Differentialgleichung
für den konformen Faktor:
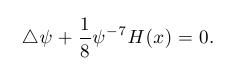
Fordert man nun
Inversionssymmetrie so ergeben sich die inneren Randbedingungen zu
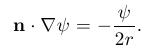
Hierbei
bezeichnet r den Radius des jeweiligen schwarzen Loches und n die äußere Normale. Die asymptotische
Flachheit spiegelt sich in der äußeren Randbedingung wieder und lässt sich
umschreiben zu:
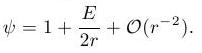
Das Gebiet
auf dem die Differentialgleichung gelöst wird, besteht aus einer Kugel mit
möglichst großem Radius aus welcher kleine Kugeln ausgeschnitten sind. Der
Radius dieser wird durch die Masse der einzelnen schwarzen Löcher
vorgegeben.
Das Problem wird durch eine modifizierte Version des Finite-Element-Programmpaketes KASKADE gelöst. Hierbei wird eine gewöhnliche Newtonschleife eingefügt, um auch das Lösen nichtlinearer, elliptischer Probleme zu ermöglichen. Eine triviale Abbruchbedingung wird dabei der Arbeit von Arup Mukherjee [2] entnommen, bei welcher der relative Fehler in jedem Punkt kleiner als 10-7 sein muß, um die Schleife zu beenden. Durch adaptive Gitterverfeinerung, flexible Zerlegung komplizierter Gebiete, effiziente Multigrid-Löser und baumartigen Datenstrukturen wird eine schnelle und genaue Lösung des Problems erwartet. Die Methode sollte hierdruch der Finite-Differenzen-Methode zumindest teilweise überlegen sein. KASKADE benutzt zur Modellierung dreidimensionaler finiter Elemente ausschließlich lineare Ansatzfunktionen auf Tetraedern.
Eine nicht zu unterschätzende Schwierigkeit stellt die Anfangszerlegung des Gebietes dar. Sie muss zur Verfügung gestellt werden. Es gibt durchaus allgemeine Gittergeneratoren, doch eine dem Problem angepasste Zerlegung ist stets vorteilhaft. Um die Approximation des Gebietes zu optimieren, werden neuen innere Randpunkte, welche durch die Verfeinerung entstehen, auf die entsprechenden Sphären projiziert. Ist die Anfangszerlegung zu grob, können während der Verfeinerung Überschneidungen von Elementen durch diese Projektion auftreten. Solche Überschneidungen sind unzulässig, zerstören Gleichungssystem und Randbedingung und bringen das Programm zum Absturz.
code validation ), da eine analytische Lösung
existiert.
In der Abbildung sind die Ergebnisse für ein schwarzes Loch mit P=0 und P=10 dargestellt. In der unteren Bildhälfte ist noch der konforme Faktor über eine der Achsen aufgetragen (Radialsymmetrische Lösung). Die dargestellte Verfeinerungstiefe dient lediglich der Visualisierung. Die verwendete Rechentechnik erlaubt höhere Verfeinerungstiefen mit bis zu vier Millionen Knoten bei akzeptabler Rechenzeit.
Man erkennt auch die regelmäßige Struktur der Elemente. Bei Verwendung von allgemeinen Gittergeneratoren sieht die Zerlung unstrukturiert aus, wie später noch erkennbar sein wird.
Da lineare Ansatzfunktionen verwendet werden, sollte der L2-Fehler zur analytischen Lösung mit h^2 und der Energiefehler mit h fallen. In der folgenden Tabelle sind L2- und Energiefehler in uniformer und adaptiver Verfeinerung dargestellt. Als Anfangszerlegung wurde dabei eine eigens erstellte verwendet und mit MESHGEN bezeichnet. Im letzten Bild sieht man, dass der Energiefehler der Anfangszerlegung von MESHGEN kleiner ist, als die des Gittergenerators NETGEN.
Im unteren Bild ist eine Vergleichsgerade proportional zu h eingetragen. Man sieht das vorerst der Energiefehler schneller fällt als vermutet. Im Falle der Anfangszerlegung durch NETGEN scheint sich der zu schnelle Abfall eher zu der asymptotischen Grenze abzuflachen. Die spezielle Anfangszerlegung ist stets besser, doch man kann auch daraus schliessen, dass NETGEN keineswegs unbrauchbar ist. Erlaubt man einen Verfeinerungsschritt mehr, so ist der Fehler in der Energienorm beider Lösungen nahezu gleich.
Die adaptive Verfeinerung im Fall eines schwarzen Loches ist nicht von Vorteil. Das kann daran liegen, dass minimaler und maximaler Winkel der Tetraederzerlegung mit jedem Verfeinerungsschritt extremer werden. Dies ist leider möglich, da durch Verfeinerung entstandene neue Randpunkte auf eine Sphäre projiziert werden. Die bei KASKADE implementierte Oktasektion bzw. Rot-Grün-Verfeinerung scheint hier wesentlich anfälliger als die Bisektion, wie man durch Vergleich mit anderen Arbeiten abschätzen kann. Nach meinem jetzigen Wissensstand existiert auch keine Arbeit, die konkret analysiert, wie bei Verfeinerung von konkaven, sphärischen Rändern zu verfahren ist.
Die Funktion H(x) lässt sich im Falle zweier schwarzer Löcher nicht einfach additiv zusammensetzen. Stattdessen erfordert die Inversionssymmetrie eine aufwendige Rechnung (siehe [3]). Analytisch ist H(x) nur durch eine unendliche Reihe darstellbar. Jedoch kann man diese Reihe schon nach wenigen Summanden abbrechen. Nichtsdestotrotz verschlingt die Berechnung von H(x) den größten Teil an Rechenzeit.
Das Gebiet stellt zwei schwarze Löcher dar. Das zweite hat dabei die doppelte Masse und dem entsprechend einen doppelt so großenThroat . Die genauen Parameter wurden der
Arbeit von Mukherjee entnommen, um die Resulate miteinander vergleichen zu
können.
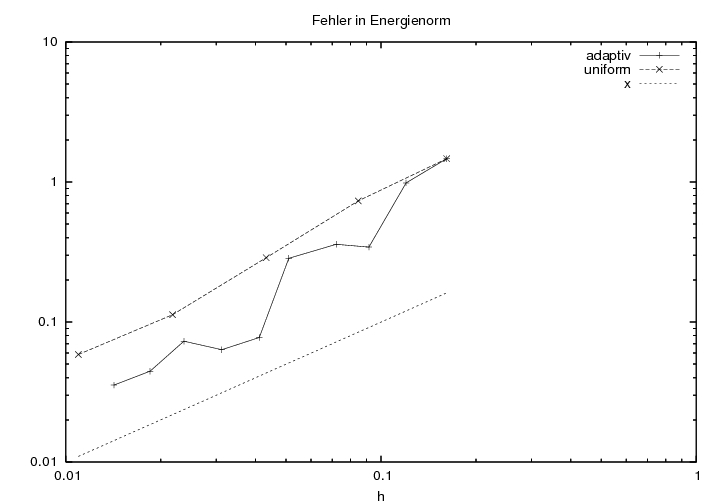
Der Energiefehler nimmt bei adaptiver Vefeinerung nun schneller ab. Zudem zeigt sich eine lineare Abnahme des Energienorm-Fehlers mit h. Eine Vergleichsgerade ist hierzu im Diagramm eingezeichnet.
Eine Verbesserung der Ergebnisse würde die Implementation der Bisektion mit sich bringen. Nicht nur, dass die konkaven, spärischen Ränder unter besseren Winkeln approximiert werden könnten. Auch verachtfacht sich nicht die Anzahl der Elemente sofort bei der Verfeinerung eines Elementes, sondern sie verdoppelt sich nur. Dadurch könnte das Gebiet effizienter verfeinert werden.
Stand: 20.Februar 2007
Die Allgemeine Relativitätstheorie wird durch die Einsteinschen Feldgleichungen dargestellt, einem System aus zehn nichtlinearen, partiellen Differentialgleichungen. Sie beschreibt die Gravitation durch die Krümmung einer vierdimensionalen, pseudoriemannschen Mannigfaltigkeit. Testteilchen auf die keine Kraft einwirkt bewegen sich dann auf Geodäten durch diesen Raum. Arnowitt, Desner und Misner schlugen eine Zerlegung in einen dreidimensionalen, raumartigen Anteil und einen eindimensionalen, zeitartigen Anteil vor. Diese 3+1-Zerlegung macht klar, dass zur Lösung des Systems partieller Differentialgleichungen Anfangsdaten auf einer Hyperfläche zu einer gewissen Zeit t notwendig sind. Abgesehen von der Topologie und dem Energie-Impuls-Tensor, welche das zu lösende Problem charakterisieren, müssen bestimmte
Betrachtet man isolierte schwarze Löcher, so gibt es keine Materie im Aussenraum und der Energie-Impuls-Tensor verschwindet. Das Gebiet auf welchem die Differentialgleichungen gelöst werden, ist nun abhängig vom jeweiligen Ansatz. Eine Variante besteht im Ausschneiden (
Anfangsdaten für schwarze Löcher
Allen hier vorgestellten Berechnungen liegt ein Gebiet mit ausgeschnittenen schwarzen Löchern zugrunde. Man setzt voraus, dass die Metrik bei hinreichend grossem Abstand flach (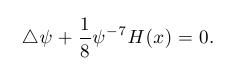
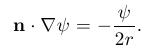
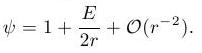
Das Problem wird durch eine modifizierte Version des Finite-Element-Programmpaketes KASKADE gelöst. Hierbei wird eine gewöhnliche Newtonschleife eingefügt, um auch das Lösen nichtlinearer, elliptischer Probleme zu ermöglichen. Eine triviale Abbruchbedingung wird dabei der Arbeit von Arup Mukherjee [2] entnommen, bei welcher der relative Fehler in jedem Punkt kleiner als 10-7 sein muß, um die Schleife zu beenden. Durch adaptive Gitterverfeinerung, flexible Zerlegung komplizierter Gebiete, effiziente Multigrid-Löser und baumartigen Datenstrukturen wird eine schnelle und genaue Lösung des Problems erwartet. Die Methode sollte hierdruch der Finite-Differenzen-Methode zumindest teilweise überlegen sein. KASKADE benutzt zur Modellierung dreidimensionaler finiter Elemente ausschließlich lineare Ansatzfunktionen auf Tetraedern.
Eine nicht zu unterschätzende Schwierigkeit stellt die Anfangszerlegung des Gebietes dar. Sie muss zur Verfügung gestellt werden. Es gibt durchaus allgemeine Gittergeneratoren, doch eine dem Problem angepasste Zerlegung ist stets vorteilhaft. Um die Approximation des Gebietes zu optimieren, werden neuen innere Randpunkte, welche durch die Verfeinerung entstehen, auf die entsprechenden Sphären projiziert. Ist die Anfangszerlegung zu grob, können während der Verfeinerung Überschneidungen von Elementen durch diese Projektion auftreten. Solche Überschneidungen sind unzulässig, zerstören Gleichungssystem und Randbedingung und bringen das Programm zum Absturz.
Ergebnisse
Die Analyse und Darstellung dreidimensionaler Ergebnisse ist interssant. Es kann nie die gesamte Information in einem Bild wiedergegeben werden da dies zweidimensional ist. Hier werden vorrangig Ebenenschnitte, normal zu eine der drei Koordinatenachsen dargestellt.Single Black Hole
Bowen und York schlugen in [1] eine Modellfunktion Hmodel vor. Sie entspricht nicht ganz physikalischen Tatsachen, eignet sich aber für die Überprüfung eines Codes (| Konformer Faktor für
ein schwarzes Loch Ebenenschnitt, x=0. Adaptive Gitterverfeinerung. H=Hmodel | |
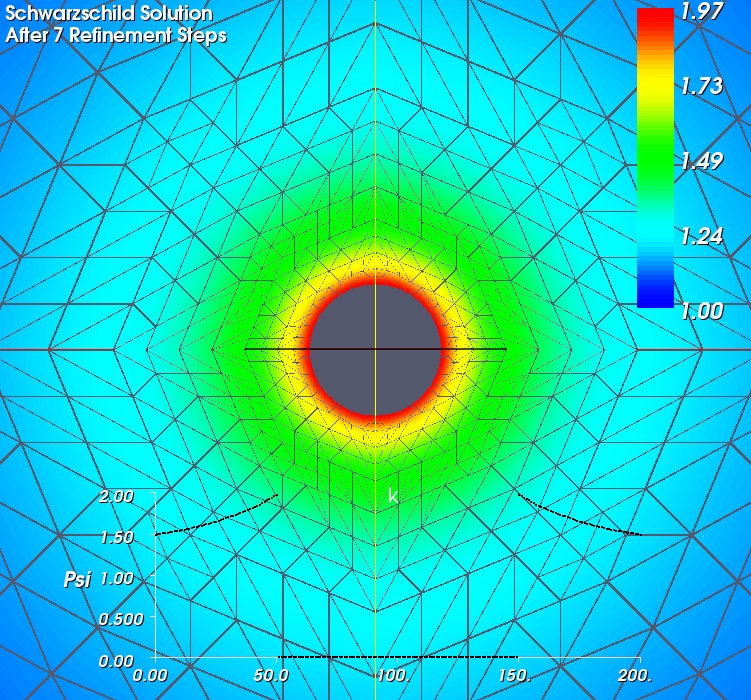 P=0 (Schwarzschild). |
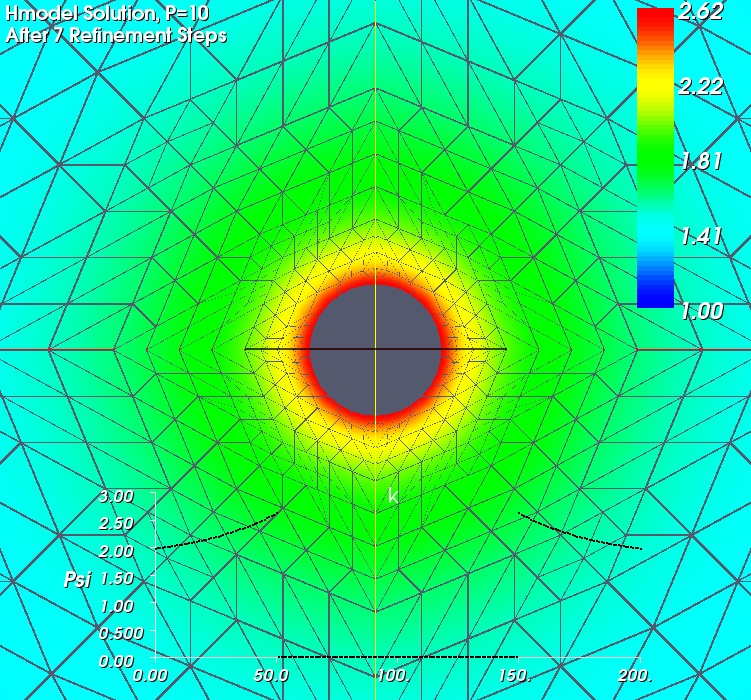 P=10. ( z.B. in z-Richtung ) |
In der Abbildung sind die Ergebnisse für ein schwarzes Loch mit P=0 und P=10 dargestellt. In der unteren Bildhälfte ist noch der konforme Faktor über eine der Achsen aufgetragen (Radialsymmetrische Lösung). Die dargestellte Verfeinerungstiefe dient lediglich der Visualisierung. Die verwendete Rechentechnik erlaubt höhere Verfeinerungstiefen mit bis zu vier Millionen Knoten bei akzeptabler Rechenzeit.
Man erkennt auch die regelmäßige Struktur der Elemente. Bei Verwendung von allgemeinen Gittergeneratoren sieht die Zerlung unstrukturiert aus, wie später noch erkennbar sein wird.
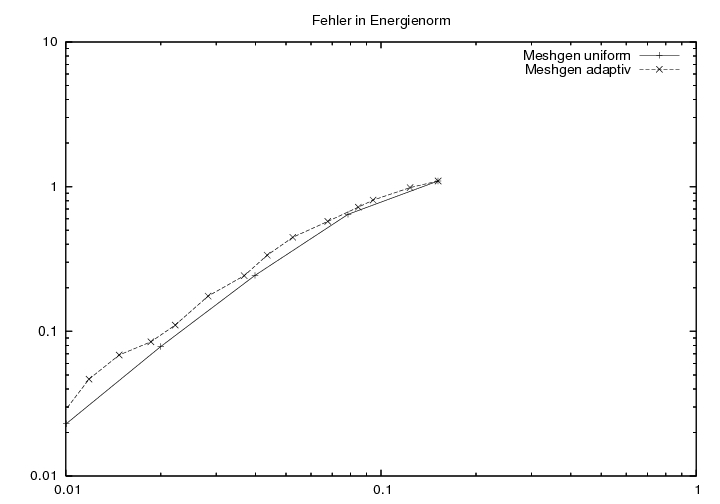
Da lineare Ansatzfunktionen verwendet werden, sollte der L2-Fehler zur analytischen Lösung mit h^2 und der Energiefehler mit h fallen. In der folgenden Tabelle sind L2- und Energiefehler in uniformer und adaptiver Verfeinerung dargestellt. Als Anfangszerlegung wurde dabei eine eigens erstellte verwendet und mit MESHGEN bezeichnet. Im letzten Bild sieht man, dass der Energiefehler der Anfangszerlegung von MESHGEN kleiner ist, als die des Gittergenerators NETGEN.
| Fehler in der Energienorm |
 |
| Fehler in L2-Norm |
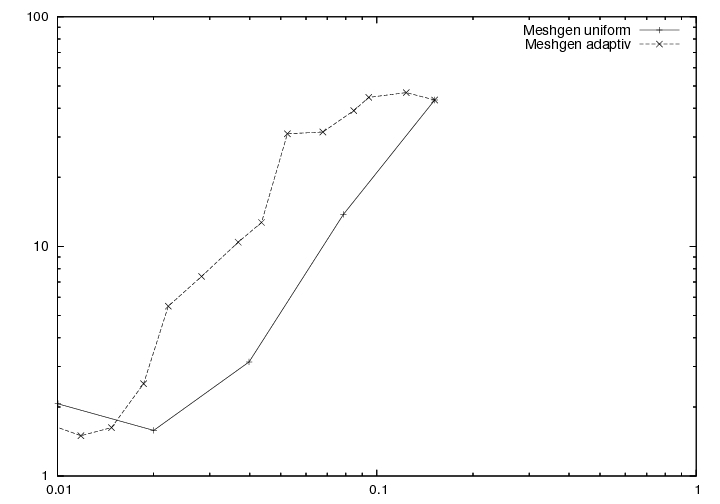 |
| Fehler in Energienorm zwischen spezieller Anfangszerlegung MESHGEN und Gittergenerator NETGEN |
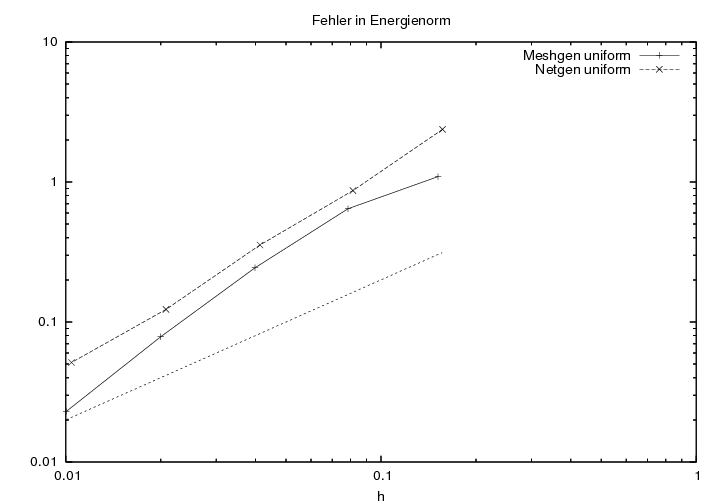 |
Im unteren Bild ist eine Vergleichsgerade proportional zu h eingetragen. Man sieht das vorerst der Energiefehler schneller fällt als vermutet. Im Falle der Anfangszerlegung durch NETGEN scheint sich der zu schnelle Abfall eher zu der asymptotischen Grenze abzuflachen. Die spezielle Anfangszerlegung ist stets besser, doch man kann auch daraus schliessen, dass NETGEN keineswegs unbrauchbar ist. Erlaubt man einen Verfeinerungsschritt mehr, so ist der Fehler in der Energienorm beider Lösungen nahezu gleich.
Die adaptive Verfeinerung im Fall eines schwarzen Loches ist nicht von Vorteil. Das kann daran liegen, dass minimaler und maximaler Winkel der Tetraederzerlegung mit jedem Verfeinerungsschritt extremer werden. Dies ist leider möglich, da durch Verfeinerung entstandene neue Randpunkte auf eine Sphäre projiziert werden. Die bei KASKADE implementierte Oktasektion bzw. Rot-Grün-Verfeinerung scheint hier wesentlich anfälliger als die Bisektion, wie man durch Vergleich mit anderen Arbeiten abschätzen kann. Nach meinem jetzigen Wissensstand existiert auch keine Arbeit, die konkret analysiert, wie bei Verfeinerung von konkaven, sphärischen Rändern zu verfahren ist.
Binary Black Hole
Die Funktion H(x) lässt sich im Falle zweier schwarzer Löcher nicht einfach additiv zusammensetzen. Stattdessen erfordert die Inversionssymmetrie eine aufwendige Rechnung (siehe [3]). Analytisch ist H(x) nur durch eine unendliche Reihe darstellbar. Jedoch kann man diese Reihe schon nach wenigen Summanden abbrechen. Nichtsdestotrotz verschlingt die Berechnung von H(x) den größten Teil an Rechenzeit.
Das Gebiet stellt zwei schwarze Löcher dar. Das zweite hat dabei die doppelte Masse und dem entsprechend einen doppelt so großen
 |
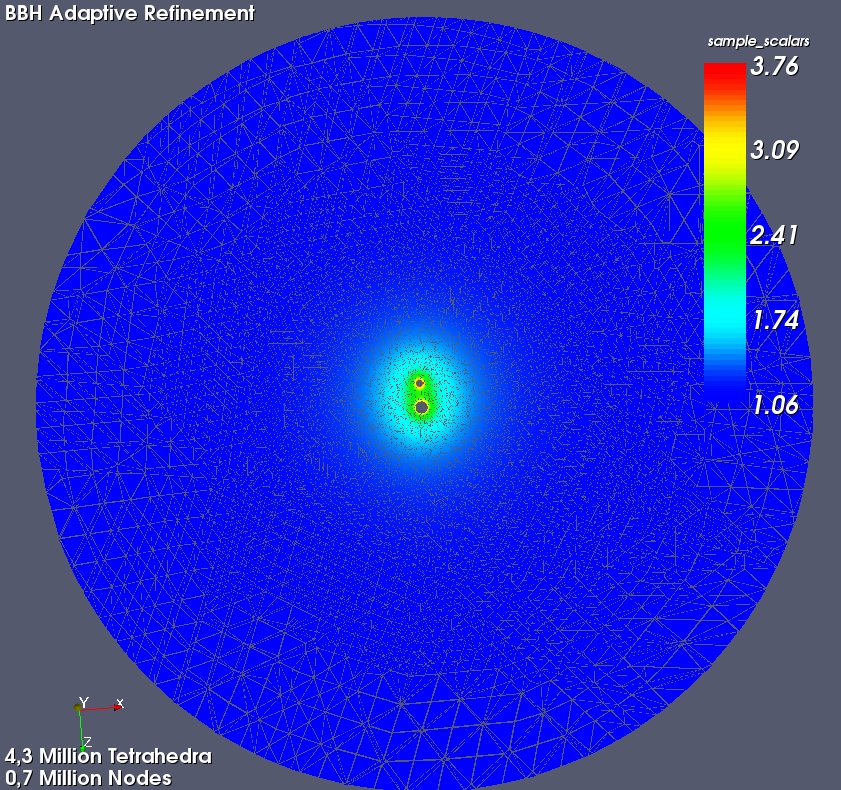 |
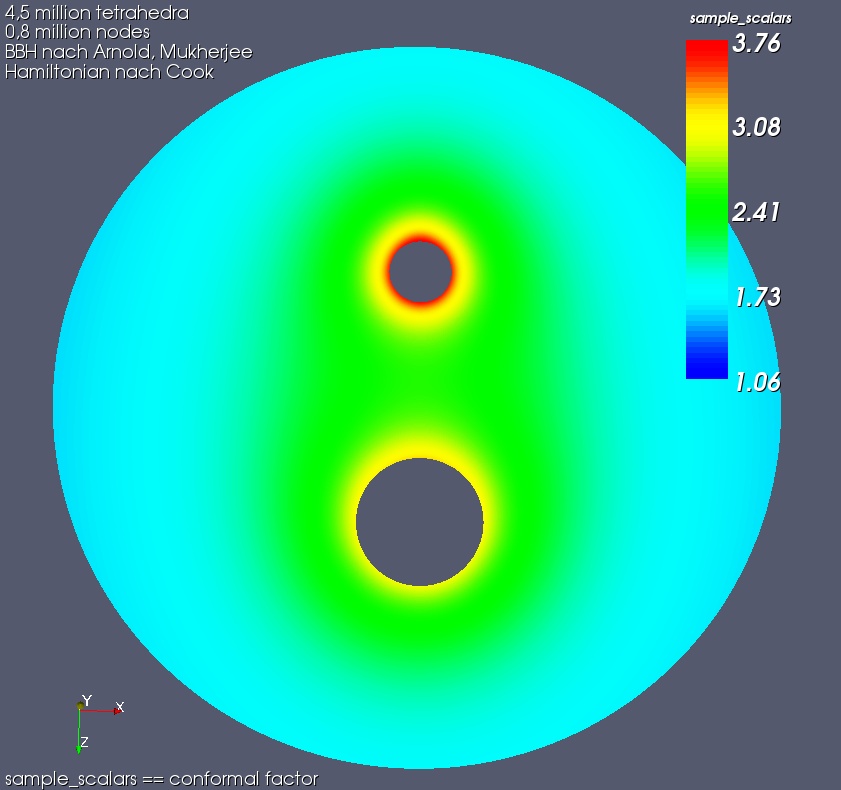
| Gebietsausschnitt. Maximale Rechentiefe. Uniforme Verfeinerung. | Gesamtes Gebiet. Maximale Rechentiefe. Adaptive Verfeinerung. |
Der Energiefehler nimmt bei adaptiver Vefeinerung nun schneller ab. Zudem zeigt sich eine lineare Abnahme des Energienorm-Fehlers mit h. Eine Vergleichsgerade ist hierzu im Diagramm eingezeichnet.

Eine Verbesserung der Ergebnisse würde die Implementation der Bisektion mit sich bringen. Nicht nur, dass die konkaven, spärischen Ränder unter besseren Winkeln approximiert werden könnten. Auch verachtfacht sich nicht die Anzahl der Elemente sofort bei der Verfeinerung eines Elementes, sondern sie verdoppelt sich nur. Dadurch könnte das Gebiet effizienter verfeinert werden.
Referenzen
| [1] | J. M. Bowen, J. W. York Jr. Time-symmetric initial data for black
holes and black-hole collisions. Phys. Rev. D 21 2047 (1980). |
| [2] | Arup Mukherjee. An Adaptive Finite Element Code For Elliptic Boundary Value Problems In Three Dimensions With Application In Numerical Relativity . PhD Thesis, 1996. |
| [3] | Gregory B. Cook. Initial data for axisymmetric black-hole collisions. Phys. Rev. D 44 2983 (1991). |
Stand: 20.Februar 2007